Acquisition automatique de Connaissances
Apprentissage par Renforcement - Q-Learning

Apprentissage et Acquisation automatique de Connaissances

Si votre système de navigation vous permet de voir (attendre le chargement et le lancement de Java platform) cette applet ? ("If you don't see the applet running, you need to install Java Plug-in, which happens automatically when you install the J2SE JRE or SDK. We strongly recommend that you install the latest version; at least 1.3.1 is required for all SUN applets. You can find more information in the Java Plug-in home page.")
Alors vous pourrez visualiser l'applet Q-Learning Tours Hanoi

1.1 Les Tours de Hanoi

C’est un problème souvent donné en exemple lors de l’apprentissage de Prolog : c’est un problème récursif de représentation simple, dont la solution peut être trouvée en 2ⁿ–1 mouvements, n étant le nombre de disques. La connaissance de la longueur optimale permet de tester l’apprentissage. Le nombre d'états est N = 3^{n + 1} (3 buts possibles).

Pour passer de l’état :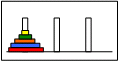

à l’état :

Il faut passer par l’état :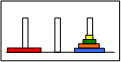

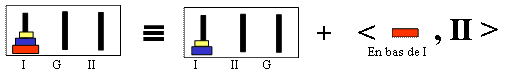
1.2 Jeux avec le problème des Tours de Hanoi :

1.2.1 Les 15 étapes sur le chemin optimal du jeu avec 4 disques :

1.2.2 Hanoï avec 2 disques ? Mémorisation

1.2.3 Résolution ? Mémorisation à long terme ? Hanoï avec 3 disques

1.3 Idée ? Ajouter deux mouvements

• oublier le plus grand disque et déplacer l'état final G, càd définition d'un sous-but ! Un sous-but est un mouvement qui fait disparaître un disque (pour ne garder que ceux concernés par ce sous-but) et qui définit l'état final de ce sous-but.
• remémorer le plus grand disque lorsqu'il n'y a rien sur sa pile (le sous-but a été atteint !) et rappeler le but précédant.

1.4 Entités manipulées

Un disque : son diamètre = son numéro de 1 à n en commençant par le plus petit;

Un état : un vecteur de 3 piles de disques, le but est le numéro de l'une d'entre elles ;

Un but : le numéro de la pile où doivent être placés les disques ;

Un mouvement autorisé : un état initial, le n° ND du disque déplacé, la pile de triplets <n°disque / n°pile en bas de laquelle il était placé / but = le n° de pile but> mémorisés, l'état final ou simplement le n° de la pile destination (cette alternative sera examinée ultérieurement) ;

Placement d'un sous-but : un mouvement autorisé particulier qui affecte la pile de triplets mémorisés : le disque déplacé est "effacé" entre l'état initial et l'état final et ce placement ajoute un triplet <n° disque / n°pile / but> ;

Effacement d'un sous but : mouvement inverse.

1.5 Jeu en partant d'une position quelconque :

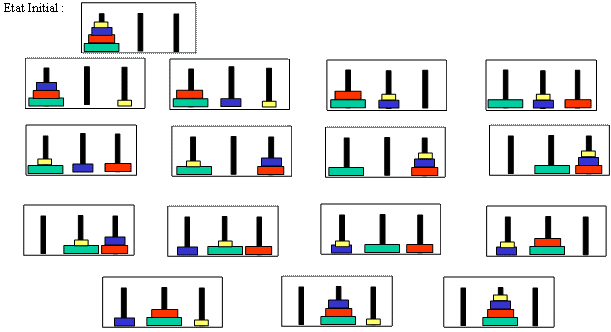
Soit l'État Initial

et le But habituel

On 'oublie' le plus grand disque

On est en présence d'un des états du jeu avec 3 disques

On retrouve un état du jeu avec 3 disques en "oubliant" le disque n et en plaçant un sous but sur la même pile.

L'exercice concernant l'application des techniques d'apprentissage par renforcement au problème des Tours de Hanoï semble adresser les sujets suivants :

• Apprentissage par renforcement en utilisant le Q-learning pour le jeu avec 3 disques, la connaissance du chemin optimal permet de tester l'apprentissage ;
• Apprentissage de la gestion de sous-buts (placement / effacement) pour ramener le problème courant à un état du problème avec 3 disques ;
• Apprentissage à long terme pour l'utilisation des solutions mémorisées (enregistrer / rechercher) des problèmes de dimension n – 1.

On pourrait ainsi comparer les résultats avec le problème avec 4 disques entre apprentissage simple ou à l'aide de sous-buts.

2.1 Représentation des entités manipulées :

2.1.1 Représentation d'un état

Taille :=4 But := II Pile n° :=I contient:= disque 3 et disque 4 Pile n° :=II contient:= disque 2 et disque 1 Pile n°:=III contient:= nil

2.1.2 Représentation du placement d'un sous but

État initial (cf. état ci-dessus),

Pile de buts := Pile de buts + <n°disque:=4/n°pile=I/but:=II>

Disque déplacé:= 4

N° de la pile destination := 0 (il faut programmer le changement de taille du problème et le changement éventuel de but)

2.1.3 Définition de la pile d'un sous-but

Si le disque n° = n = dimension du problème est sur une pile n°X =/= n° pile but = Y, il faut placer le sous-but en Z,

Si ce disque est déjà sur la pile but il faut placer le sous-but sur cette même pile.

2.1.4 Symétrie

Les deux piles non-but jouent un rôle équivalent tant qu'on n'introduit pas de gestion de sous-but. Aujourd'hui je suis tenté de ne pas tenir compte des symétries.

3.1 Description du RL

Le programme indique au système quel est le but à atteindre et ce système doit apprendre par une succession d'essais/erreurs comment atteindre ce but. Le système est connecté à son environnement par des perceptions et des actions. A chaque interaction, l'agent reçoit une information relative à son état courant s, il choisit et effectue une action a qui le fait passer dans un état s', et il reçoit un signal de renforcement.

3.2 Elements constitutifs

La politique p : S -> A : application des états dans les actions;

La récompense immédiate r : S x A -> [0, 1] indicateur immédiat de la qualité d'une action dans un état s ;
"Les conséquences futures d'une action ne sont pas incluses dans le renforcement reçu, mais peuvent avoir une influence non négligeable sur l'ensemble des interactions."
On cherche à optimiser l'espérance des récompenses à 'horizon fini' ou à 'horizon infini'.

La fonction valeur indicateur de la valeur du choix à long terme
"On peut calculer la valeur d'une action dans un état s suivant une politique p, quantité notée Q^p(s, a) comme l'espérance en partant de l'état s et choisissant l'action a puis en suivant la politique p."

Le Q-Learning a été développé "afin de déterminer une politique optimale p* sans disposer de toutes les données".

3.3 Algorithme du Q-Learning

Pour chaque couple <s,a> initialiser le vecteur Q(s, a) à 0;
t:= 0; s₀ := état initial;
Répéter
Exit quand s_t est un état terminal
Choisir une action a_t dans A(s_t)   //Explore vs Exploite
Exécuter a_t
Q(s_t,a_t) := (1 - a) * Q(s_t,a_t)
+ a(r(s_t,a_t) + g * Max Q(s_t+1,a_t+1)); // Max = max sur a_t+1 Î A(s_t+1)
t := t+1;
End Répéter

a est un taux de changement et g est un taux d'interet

Applet Q-Learning Tours Hanoi

Convergence de l'apprentissage par Q-Learning

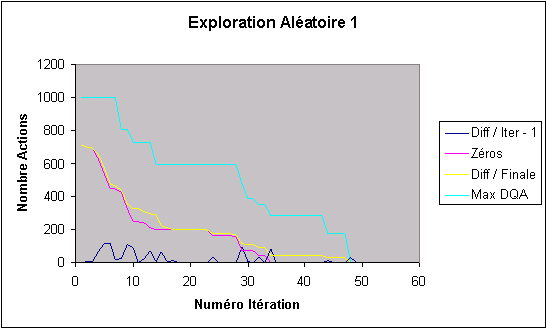
Courbe donnant le nombre d'actions dont la valeur est différente de celle qu'elle avait à l'itération précédante.

La longueur du chemin optimal est égale à 2ⁿ-1, donc égale à 15 pour n = 4. Le nombre d'itérations d'exploration pour 4 disques doit donc être supérieur à 15.

Les deux figures suivantes correspondent aux résultats de deux lancements de 50 itérations d'exploration effectuées chacune avec chacun des trois buts, les 4 disques étant tous placés sur une pile choisie aléatoirement. Pour les deux courbes ci-dessous :

• Diff / Iter – 1 représente le nombre d'actions dont la valeur est différente de celle obtenue à l'itération précédante ;
• Zéros représente le nombre d'actions dont la valeur est encore égale à 0 ;
• Diff / Finale représente le nombre d'actions dont la valeur est différente de celle obtenue lors d'une exploration antérieure après 100 itérations ;
• Max DQA représente la plus grande différence entre la valeur d'une action à l'itération et la valeur obtenue lors d'une exploration antérieure après 100 itérations : c'est une mesure de la convergence.

6.1 Q-Learning

Le problème des Tours de Hanoi est un bon exemple pour l'Apprentissage par Renforcement, ses caractéristiques correspondent aux réponses à la question principale :

Quand doit-on faire appel à l'apprentissage par renforcement ? (tâche en plusieurs étapes, la récompense ne vient qu'à la fin d'une succession de choix, …)

Pour l'apprentissage sans gestion de sous-but, l'algorithme Q-Learning permettant d'apprendre la fonction d'utilité liée aux actions a été utilisé. C'est un algorithme très simple.

6.2 Apprentissage à Long Terme

La notion d'apprentissage à long terme a pu être testée. Il est facile d'enregistrer les résultats d'une phase d'exploration.

6.3 La gestion de sous-but

Elle a été implémentée par programmation : Pour chaque état du problème avec 4 disques (la généralisation à n disques ne poserait aucun problème particulier), une action qui permet de passer au problème avec 3 disques avec nouveau but est définie dans le code de l'exécution de l'action. Le logiciel utilise alors les résultats de l'apprentissage du problème avec 3 disques pour atteindre le sous-but.

Acquisition Automatique de Connaissances, quelques liens

L'objectif de ce site est de décrire simplement (clairement autant que faire se peut) les différentes techniques de Représentation des Connaissances et leur utilisation dans les domaines de la Gestion des Connaissances et de l'Intelligence Économique. N'hésitez pas à nous contacter pour proposer un simple échange de liens ou la diffusion d'un texte pédagogique sur une de ces techniques.

• Thème APA : Apprentissage et Acquisition des Connaissances